SVG - 路径path的贝塞尔曲线指令
更新日期:
SVG - 路径path的贝塞尔曲线指令
贝塞尔曲线基本概要
“贝塞尔曲线” 可以绘制任何曲线,包括直线。
贝塞尔曲线的兄弟姐妹有点多:线性贝塞尔曲线、二次方贝塞尔曲线、三次方贝塞尔曲线、四次方贝塞尔曲线、五次方贝塞尔曲线、……。

线性贝塞尔曲线演示动画,t在[0,1]区间
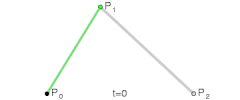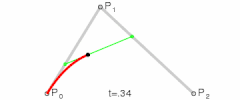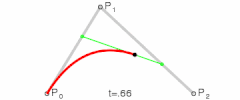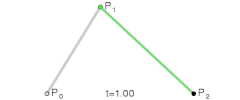
二次贝塞尔曲线演示动画,t在[0,1]区间

三次贝塞尔曲线演示动画,t在[0,1]区间
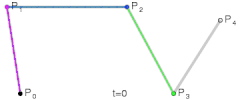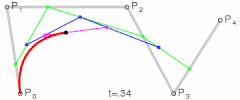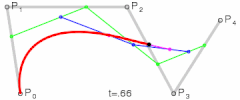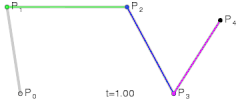
四次贝塞尔曲线演示动画,t在[0,1]区间

五次贝塞尔曲线演示动画,t在[0,1]区间
以上动图都是基于数学公式,目前阶段接触公式不利于我们的学习,因此,大家感受一下就可以了。
SVG贝塞尔曲线指令概要
SVG中path的元素,也就是路径绘制,属性名称是d, 具体值是由专门的“指令字母+坐标值”实现的,例如下面这个简单代码示意:
<path d="M10 10L90 90" stroke="#000000" style="stroke-width: 5px;"></path>
标准的指令字母是10个,外加1个非标准的
| 命令 | 名称 | 参数 |
|---|---|---|
| M | moveto 移动到 | (x y)+ |
| Z | closepath 关闭路径 | (none) |
| L | lineto 画线到 | (x y)+ |
| H | horizontal lineto 水平线到 | x+ |
| V | vertical lineto 垂直线到 | y+ |
| C | curveto 三次贝塞尔曲线到 | (x1 y1 x2 y2 x y)+ |
| S | smooth curveto 光滑三次贝塞尔曲线到 | (x2 y2 x y)+ |
| Q | quadratic Bézier curveto 二次贝塞尔曲线到 | (x1 y1 x y)+ |
| T | smooth quadratic Bézier curveto 光滑二次贝塞尔曲线到 | (x y)+ |
| A | elliptical arc 椭圆弧 | (rx ry x-axis-rotation large-arc-flag sweep-flag x y)+ |
| R | Catmull-Rom curveto* Catmull-Rom曲线 | x1 y1 (x y)+ |
其中,Catmull-Rom曲线不是标准的SVG命令。
如果指令字母是大写的,例如M, 则表示坐标位置是绝对位置;如果指令字母小写的,例如m, 则表示坐标位置是相对位置。
其中,有5个指定属于基本指令,你也可以理解为“好理解好上手好记忆”的指令,见下表:
| 指令字母(绝对坐标) | 中文含义 | 参数示意 | 具体说明 |
|---|---|---|---|
| M | 移动到(moveTo) | x,y | 路径起始点坐标 |
| Z | 闭合路径(closepath) | 将路径的开始和结束点用直线连接 | |
| L | 直线(lineTo) | x,y | 当前节点到指定(x,y)节点,直线连接 |
| H | 水平直线 | x | 保持当前点的y坐标不变,x轴移动到x, 形成水平线 |
| V | 垂直直线 | y | 保持当前点的x坐标不变,y轴移动到y, 形成垂直线 |
除了这5个参数及直来直往的指令,剩下的,除了弧形命令A(Arcs),就都是与贝塞尔曲线相关的命令了, 合称“厕所切图(CSQT)”。
CS 组合 和 QT组合
- CS:三次贝塞尔曲线
- QT:二次贝塞尔曲线
三次贝塞尔曲线需要定义一个点和两个控制点,所以用C命令创建三次贝塞尔曲线,需要设置三组坐标参数
C x1 y1, x2 y2, x y (or c dx1 dy1, dx2 dy2, dx dy)

这里的最后一个坐标(x,y)表示的是曲线的终点,另外两个坐标是控制点,(x1,y1)是起点的控制点,(x2,y2)是终点的控制点。
示例:
<svg width="190px" height="160px" version="1.1" xmlns="http://www.w3.org/2000/svg">
<path d="M10 10 C 20 20, 40 20, 50 10" stroke="black" fill="transparent"/>
<path d="M70 10 C 70 20, 120 20, 120 10" stroke="black" fill="transparent"/>
<path d="M130 10 C 120 20, 180 20, 170 10" stroke="black" fill="transparent"/>
<path d="M10 60 C 20 80, 40 80, 50 60" stroke="black" fill="transparent"/>
<path d="M70 60 C 70 80, 110 80, 110 60" stroke="black" fill="transparent"/>
<path d="M130 60 C 120 80, 180 80, 170 60" stroke="black" fill="transparent"/>
<path d="M10 110 C 20 140, 40 140, 50 110" stroke="black" fill="transparent"/>
<path d="M70 110 C 70 140, 110 140, 110 110" stroke="black" fill="transparent"/>
<path d="M130 110 C 120 140, 180 140, 170 110" stroke="black" fill="transparent"/>
</svg>
效果图:

你可以将若干个贝塞尔曲线连起来,从而创建出一条很长的平滑曲线。如果将一个点的控制点在它的另一侧建立一个对称点(斜率不变),可以通过一个简写的命令来实现,这个命令是S(或s)。(这段话可以这样理解:S命令前面可以是一条C命令创建的三次贝赛尔曲线,这时候,S命令跟在C命令的后面,就可以用比较简单的参数,生成一个与前面那个相对称的三次贝塞尔曲线。仔细看一下后面的图例,可以帮助理解。另外,S命令也可以跟在S命令后面。)
S x2 y2, x y (or s dx2 dy2, dx dy)
S命令可以用来创建与之前那些曲线一样的贝塞尔曲线,但是,如果S命令跟在一个C命令或者另一个S命令的后面,它的第一个控制点,就会被假设成前一个控制点的对称点。如果S命令单独使用,前面没有C命令或者另一个S命令,那么它的两个控制点就会被假设为同一个点(其表现就跟二次贝塞尔曲线的Q一模一样)。下面是S命令的语法示例,如图所示,左侧的控制点用红色标示,与它对称的控制点用蓝色标示。
示例:
<svg width="190px" height="160px" version="1.1" xmlns="http://www.w3.org/2000/svg">
<path d="M10 80 C 40 10, 65 10, 95 80 S 150 150, 180 80" stroke="black" fill="transparent"/>
</svg>
效果图:

大家要把关注点放在蓝线上面。S指令会自动补出一个对称的控制点(蓝线部分)。于是,就会有连续的平滑曲线啦!
二次贝塞尔曲线Q,它比三次贝塞尔曲线简单,只需要一个控制点,用来确定起点和终点的曲线斜率。因此它需要两组参数,控制点和终点坐标。
Q x1 y1, x y (or q dx1 dy1, dx dy)
示例:
<svg width="190px" height="160px" version="1.1" xmlns="http://www.w3.org/2000/svg"">
<path d="M10 80 Q 95 10 180 80" stroke="black" fill="transparent"/>
</svg>
效果图:

就像三次贝塞尔曲线有一个S命令,二次贝塞尔曲线有一个差不多的T命令,可以通过更简短的参数,延长二次贝塞尔曲线。
T x y (or t dx dy)
和之前一样,快捷命令T会通过前一个控制点,推断出一个新的控制点。这意味着,在你的第一个控制点后面,可以只定义终点,就创建出一个相当复杂的曲线。需要注意的是,T命令前面必须是一个Q命令,或者是另一个T命令,才能达到这种效果。如果T单独使用,那么控制点就会被认为和终点是同一个点,所以画出来的将是一条直线。
示例:
<svg width="190px" height="160px" version="1.1" xmlns="http://www.w3.org/2000/svg">
<path d="M10 80 Q 52.5 10, 95 80 T 180 80" stroke="black" fill="transparent"/>
</svg>
效果图:

虽然三次贝塞尔曲线拥有更大的自由度,但是两种曲线能达到的效果总是差不多的。具体使用哪种曲线,通常取决于需求,以及对曲线对称性的依赖程度。
